Portal:Mathematics
- አማርኛ
- العربية
- Avañe'ẽ
- Авар
- تۆرکجه
- বাংলা
- 閩南語 / Bân-lâm-gú
- Беларуская (тарашкевіца)
- Bikol Central
- Български
- Català
- Cebuano
- Čeština
- الدارجة
- Deutsch
- Eesti
- Ελληνικά
- Español
- فارسی
- Français
- Gĩkũyũ
- 한국어
- Hausa
- Հայերեն
- हिन्दी
- Bahasa Indonesia
- Interlingua
- Íslenska
- Italiano
- עברית
- ქართული
- Қазақша
- Kiswahili
- Kreyòl ayisyen
- Kurdî
- Latina
- Lietuvių
- Magyar
- Македонски
- Malti
- مصرى
- ဘာသာမန်
- Bahasa Melayu
- မြန်မာဘာသာ
- Nederlands
- 日本語
- Oʻzbekcha / ўзбекча
- ਪੰਜਾਬੀ
- پښتو
- Picard
- Polski
- Português
- Română
- Runa Simi
- Русский
- Shqip
- සිංහල
- سنڌي
- Slovenčina
- Soomaaliga
- کوردی
- Српски / srpski
- Suomi
- Svenska
- தமிழ்
- Taclḥit
- Татарча / tatarça
- ၽႃႇသႃႇတႆး
- ไทย
- Тоҷикӣ
- Türkçe
- Українська
- اردو
- Tiếng Việt
- 文言
- 吴语
- ייִדיש
- Yorùbá
- 粵語
- Zazaki
- 中文
- Batak Mandailing
- ⵜⴰⵎⴰⵣⵉⵖⵜ ⵜⴰⵏⴰⵡⴰⵢⵜ
Tools
Actions
General
Print/export
In other projects
Appearance
Portal maintenance status: (December 2018)
|
Wikipedia portal for content related to Mathematics
-
Abacus, a ancient hand-operated calculating.
-
Portrait of Emmy Noether, around 1900.
Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)
Featured articles
-
Image 1
Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ⓘ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.
Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...) -
Image 2Portrait by Jakob Emanuel Handmann, 1753
Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] ⓘ, Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.
Euler is credited for popularizing the Greek letter(lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation
for the value of a function, the letter
to express the imaginary unit
, the Greek letter
(capital sigma) to express summations, the Greek letter
(capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant
, the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...)
-
Image 3Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.
An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.
While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in the 17th century studies of probability and annuities. Actuaries of the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems to design programs that manage risk, by determining if the implementation of strategies proposed for mitigating potential risks, does not exceed the expected cost of those risks actualized. The steps needed to become an actuary, including education and licensing, are specific to a given country, with various additional requirements applied by regional administrative units; however, almost all processes impart universal principles of risk assessment, statistical analysis, and risk mitigation, involving rigorously structured training and examination schedules, taking many years to complete. (Full article...) -
Image 4
Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She also proved Noether's first and second theorems, which are fundamental in mathematical physics. Noether was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.
Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...) -
Image 5A stamp of Zhang Heng issued by China Post in 1955
Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Eastern Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.
Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...) -
Image 6

Logic studies valid forms of inference like modus ponens.
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.
Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like(and) or
(if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
-
Image 7
Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.
Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...) -
Image 8

Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.
In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).
In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...) -
Image 9
The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.
Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...) -
Image 10

Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...) -
Image 11Elementary algebra studies which values solve equations formed using arithmetical operations.
Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.
Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...) -
Image 12

The weighing pans of this balance scale contain zero objects, divided into two equal groups.
In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...) -
Image 13The title page of a 1634 version of Hues' Tractatus de globis in the collection of the Biblioteca Nacional de Portugal
Robert Hues (1553 – 24 May 1632) was an English mathematician and geographer. He attended St. Mary Hall at Oxford, and graduated in 1578. Hues became interested in geography and mathematics, and studied navigation at a school set up by Walter Raleigh. During a trip to Newfoundland, he made observations which caused him to doubt the accepted published values for variations of the compass. Between 1586 and 1588, Hues travelled with Thomas Cavendish on a circumnavigation of the globe, performing astronomical observations and taking the latitudes of places they visited. Beginning in August 1591, Hues and Cavendish again set out on another circumnavigation of the globe. During the voyage, Hues made astronomical observations in the South Atlantic, and continued his observations of the variation of the compass at various latitudes and at the Equator. Cavendish died on the journey in 1592, and Hues returned to England the following year.
In 1594, Hues published his discoveries in the Latin work Tractatus de globis et eorum usu (Treatise on Globes and Their Use) which was written to explain the use of the terrestrial and celestial globes that had been made and published by Emery Molyneux in late 1592 or early 1593, and to encourage English sailors to use practical astronomical navigation. Hues' work subsequently went into at least 12 other printings in Dutch, English, French and Latin. (Full article...) -
Image 14One of Molyneux's celestial globes, which is displayed in Middle Temple Library – from the frontispiece of the Hakluyt Society's 1889 reprint of A Learned Treatise of Globes, both Cœlestiall and Terrestriall, one of the English editions of Robert Hues' Latin work Tractatus de Globis (1594)
Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.
Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...) -
Image 15
Theodore John Kaczynski (/kəˈzɪnski/ ⓘ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ ⓘ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle.
Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored Industrial Society and Its Future, a 35,000-word manifesto and social critique opposing all forms of technology, rejecting leftism, and advocating a nature-centered form of anarchism. (Full article...)
Good articles
-
Image 1

A Pythagorean tiling
A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles. When used for this, it is also known as a hopscotch pattern or pinwheel pattern,
but it should not be confused with the mathematical pinwheel tiling, an unrelated pattern.
This tiling has four-way rotational symmetry around each of its squares. When the ratio of the side lengths of the two squares is an irrational number such as the golden ratio, its cross-sections form aperiodic sequences with a similar recursive structure to the Fibonacci word. Generalizations of this tiling to three dimensions have also been studied. (Full article...) -
Image 2The small set expansion hypothesis or small set expansion conjecture in computational complexity theory is an unproven computational hardness assumption. Under the small set expansion hypothesis it is assumed to be computationally infeasible to distinguish between a certain class of expander graphs called "small set expanders" and other graphs that are very far from being small set expanders. This assumption implies the hardness of several other computational problems, and the optimality of certain known approximation algorithms.
The small set expansion hypothesis is related to the unique games conjecture, another unproven computational hardness assumption according to which accurately approximating the value of certain games is computationally infeasible. If the small set expansion hypothesis is true, then so is the unique games conjecture. (Full article...) -
Image 3

A set of 20 points in a 10 × 10 grid, with no three points in a line.
The no-three-in-line problem in discrete geometry asks how many points can be placed in thegrid so that no three points lie on the same line. The problem concerns lines of all slopes, not only those aligned with the grid. It was introduced by Henry Dudeney in 1900. Brass, Moser, and Pach call it "one of the oldest and most extensively studied geometric questions concerning lattice points".
At mostpoints can be placed, because
points in a grid would include a row of three or more points, by the pigeonhole principle. Although the problem can be solved with
points for every
up to
, it is conjectured that fewer than
points can be placed in grids of large size. Known methods can place linearly many points in grids of arbitrary size, but the best of these methods place slightly fewer than
points, not
. (Full article...)
-
Image 4
Summa de arithmetica, geometria, proportioni et proportionalita (Summary of arithmetic, geometry, proportions and proportionality) is a book on mathematics written by Luca Pacioli and first published in 1494. It contains a comprehensive summary of Renaissance mathematics, including practical arithmetic, basic algebra, basic geometry and accounting, written for use as a textbook and reference work.
Written in vernacular Italian, the Summa is the first printed work on algebra, and it contains the first published description of the double-entry bookkeeping system. It set a new standard for writing and argumentation about algebra, and its impact upon the subsequent development and standardization of professional accounting methods was so great that Pacioli is sometimes referred to as the "father of accounting". (Full article...) -
Image 5
Arnold Ephraim Ross (August 24, 1906 – September 25, 2002) was a mathematician and educator who founded the Ross Mathematics Program, a number theory summer program for gifted high school students. He was born in Chicago, but spent his youth in Odesa, Ukraine, where he studied with Samuil Shatunovsky. Ross returned to Chicago and enrolled in University of Chicago graduate coursework under E. H. Moore, despite his lack of formal academic training. He received his Ph.D. and married his wife, Bee, in 1931.
Ross taught at several institutions including St. Louis University before becoming chair of University of Notre Dame's mathematics department in 1946. He started a teacher training program in mathematics that evolved into the Ross Mathematics Program in 1957 with the addition of high school students. The program moved with him to Ohio State University when he became their department chair in 1963. Though forced to retire in 1976, Ross ran the summer program until 2000. He had worked with over 2,000 students during more than forty summers. (Full article...) -
Image 6In control system theory, and various branches of engineering, a transfer function matrix, or just transfer matrix is a generalisation of the transfer functions of single-input single-output (SISO) systems to multiple-input and multiple-output (MIMO) systems. The matrix relates the outputs of the system to its inputs. It is a particularly useful construction for linear time-invariant (LTI) systems because it can be expressed in terms of the s-plane.
In some systems, especially ones consisting entirely of passive components, it can be ambiguous which variables are inputs and which are outputs. In electrical engineering, a common scheme is to gather all the voltage variables on one side and all the current variables on the other regardless of which are inputs or outputs. This results in all the elements of the transfer matrix being in units of impedance. The concept of impedance (and hence impedance matrices) has been borrowed into other energy domains by analogy, especially mechanics and acoustics. (Full article...) -
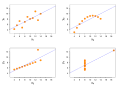
Image 7

The Theil–Sen estimator of a set of sample points with outliers (black line) compared to the non-robust ordinary least squares line for the same set (blue). The dashed green line represents the ground truth from which the samples were generated.
In non-parametric statistics, the Theil–Sen estimator is a method for robustly fitting a line to sample points in the plane (simple linear regression) by choosing the median of the slopes of all lines through pairs of points. It has also been called Sen's slope estimator, slope selection, the single median method, the Kendall robust line-fit method, and the Kendall–Theil robust line. It is named after Henri Theil and Pranab K. Sen, who published papers on this method in 1950 and 1968 respectively, and after Maurice Kendall because of its relation to the Kendall tau rank correlation coefficient.
Theil-Sen regression has several advantages over Ordinary least squares regression. It is insensitive to outliers. It can be used for significance tests even when residuals are not normally distributed. It can be significantly more accurate than non-robust simple linear regression (least squares) for skewed and heteroskedastic data, and competes well against least squares even for normally distributed data in terms of statistical power. It has been called "the most popular nonparametric technique for estimating a linear trend". There are fast algorithms for efficiently computing the parameters. (Full article...) -
Image 8

The square root of 2 is equal to the length of the hypotenuse of a right triangle with legs of length 1 and is therefore a constructible number
In geometry and algebra, a real numberis constructible if and only if, given a line segment of unit length, a line segment of length
can be constructed with compass and straightedge in a finite number of steps. Equivalently,
is constructible if and only if there is a closed-form expression for
using only integers and the operations for addition, subtraction, multiplication, division, and square roots.
The geometric definition of constructible numbers motivates a corresponding definition of constructible points, which can again be described either geometrically or algebraically. A point is constructible if it can be produced as one of the points of a compass and straightedge construction (an endpoint of a line segment or crossing point of two lines or circles), starting from a given unit length segment. Alternatively and equivalently, taking the two endpoints of the given segment to be the points (0, 0) and (1, 0) of a Cartesian coordinate system, a point is constructible if and only if its Cartesian coordinates are both constructible numbers.[1] Constructible numbers and points have also been called ruler and compass numbers and ruler and compass points, to distinguish them from numbers and points that may be constructed using other processes. (Full article...) -
Image 9

The convex hull of the red set is the blue and red convex set.
In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.
Convex hulls of open sets are open, and convex hulls of compact sets are compact. Every compact convex set is the convex hull of its extreme points. The convex hull operator is an example of a closure operator, and every antimatroid can be represented by applying this closure operator to finite sets of points.
The algorithmic problems of finding the convex hull of a finite set of points in the plane or other low-dimensional Euclidean spaces, and its dual problem of intersecting half-spaces, are fundamental problems of computational geometry. They can be solved in timefor two or three dimensional point sets, and in time matching the worst-case output complexity given by the upper bound theorem in higher dimensions. (Full article...)
-
Image 10In geometry, the Dehn invariant is a value used to determine whether one polyhedron can be cut into pieces and reassembled ("dissected") into another, and whether a polyhedron or its dissections can tile space. It is named after Max Dehn, who used it to solve Hilbert's third problem by proving that certain polyhedra with equal volume cannot be dissected into each other.
Two polyhedra have a dissection into polyhedral pieces that can be reassembled into either one, if and only if their volumes and Dehn invariants are equal. Having Dehn invariant zero is a necessary (but not sufficient) condition for being a space-filling polyhedron, and a polyhedron can be cut up and reassembled into a space-filling polyhedron if and only if its Dehn invariant is zero. The Dehn invariant of a self-intersection-free flexible polyhedron is invariant as it flexes. Dehn invariants are also an invariant for dissection in higher dimensions, and (with volume) a complete invariant in four dimensions. (Full article...) -
Image 11
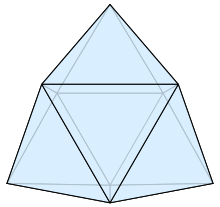
The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron, composite polyhedron, and Johnson solid.
The edges and vertices of the triaugmented triangular prism form a maximal planar graph with 9 vertices and 21 edges, called the Fritsch graph. It was used by Rudolf and Gerda Fritsch to show that Alfred Kempe's attempted proof of the four color theorem was incorrect. The Fritsch graph is one of only six graphs in which every neighborhood is a 4- or 5-vertex cycle. (Full article...) -
Image 12

The Petersen graph is the smallest snark.
In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.
One of the equivalent forms of the four color theorem is that every snark is a non-planar graph. Research on snarks originated in Peter G. Tait's work on the four color theorem in 1880, but their name is much newer, given to them by Martin Gardner in 1976. Beyond coloring, snarks also have connections to other hard problems in graph theory: writing in the Electronic Journal of Combinatorics, Miroslav Chladný and Martin Škoviera state thatAs well as the problems they mention, W. T. Tutte's snark conjecture concerns the existence of Petersen graphs as graph minors of snarks; its proof has been long announced but remains unpublished, and would settle a special case of the existence of nowhere zero 4-flows. (Full article...)
Did you know
- ... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?
- ... that in 1967 two mathematicians published PhD dissertations independently disproving the same thirteen-year-old conjecture?
- ... that Ewa Ligocka cooked another mathematician's goose?
- ... that Fathimath Dheema Ali is the first Olympic qualifier from the Maldives?
- ... that the word algebra is derived from an Arabic term for the surgical treatment of bonesetting?
- ... that multiple mathematics competitions have made use of Sophie Germain's identity?
- ... that two members of the French parliament were killed when a delayed-action German bomb exploded in the town hall at Bapaume on 25 March 1917?
- ... that people in Madagascar perform algebra on tree seeds in order to tell the future?

- ...that as of April 2010 only 35 even numbers have been found that are not the sum of two primes which are each in a Twin Primes pair? ref
- ...the Piphilology record (memorizing digits of Pi) is 70000 as of Mar 2015?
- ...that people are significantly slower to identify the parity of zero than other whole numbers, regardless of age, language spoken, or whether the symbol or word for zero is used?
- ...that Auction theory was successfully used in 1994 to sell FCC airwave spectrum, in a financial application of game theory?
- ...properties of Pascal's triangle have application in many fields of mathematics including combinatorics, algebra, calculus and geometry?
- ...work in artificial intelligence makes use of swarm intelligence, which has foundations in the behavioral examples found in nature of ants, birds, bees, and fish among others?
- ...that statistical properties dictated by Benford's Law are used in auditing of financial accounts as one means of detecting fraud?
Showing 7 items out of 75
Featured pictures
-
Image 1Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 2Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 3Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 4Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 5Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 6Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 8Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 10Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 11Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 13Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 14Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 15Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 16Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 17Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 18Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 20Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 22Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 23Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 24Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 25Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 26Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 28Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 29Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 31Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 32Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 33Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 34Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Get involved
- For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.
Categories
Topics
Index of articles
| ARTICLE INDEX: | |
| MATHEMATICIANS: |
Vital articles
- » subpages: Level 4 Mathematics articles, Level 5 Mathematics articles
Discover Wikipedia using portals
- ^ Kazarinoff (2003), pp. 10, 15 sfnmp error: no target: CITEREFKazarinoff2003 (help); Martin (1998), p. 41, Corollary 2.16 sfnmp error: no target: CITEREFMartin1998 (help).
Hidden categories:
- Pages using the Phonos extension
- Pages with Polish IPA
- Pages including recorded pronunciations
- Pages with German IPA
- Pages with Swiss Standard German IPA
- Wikipedia semi-protected portals
- Manually maintained portal pages from December 2018
- All manually maintained portal pages
- Portals with triaged subpages from December 2018
- All portals with triaged subpages
- Portals with named maintainer
- Wikipedia move-protected portals
- Automated article-slideshow portals with 31–40 articles in article list
- Automated article-slideshow portals with 101–200 articles in article list
- Random portal component with over 50 available subpages




![Image 1 Rejewski, c. 1932 Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ⓘ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence. Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)](http://upload.wikimedia.org/wikipedia/en/d/d2/Blank.png)